Loss Functions

The Mask R-CNN loss function is a combination of classification loss $L_{cls}$, bounding box loss $L_{box}$, and mask loss $L_{mask}$, \(L = L_{cls}+L_{box}+L_{mask}\)

Classification Loss

• $L_{cls}(p, u) = -log p_u$ Log Loss
• $p$, for each ROI discrete probability distribution over all categories ($p = (p_0, …, p_k)$)
• $u$ is ground truth class (0 for background and 1, 2, 3 etc otherwise)
• $p_u$ is $u^{th}$ element of $p$

Bounding Box Loss

• $L_{box}(t^u, v) = [u \geq 1] \sum_{i \in {x, y,w, h}} smooth_{L1}(t_i^u-v_i)$
• $[u \geq 1]$, 0 for background, 1 otherwise (Iverson bracket)
• $t^u$ is bounding box regression offsets for class $u$ consisitng of ($x, y, w, h$ )
• $v$ is ground truth bounding box regression target

Mask Loss

• $L_{mask}$ BCE calculated only for ground truth category mask (sum is over all pixels)
• $BCE = -\frac{1}{N} \sum^{N}_{i=1}[y_i log(p_i) + (1-y_i)]$

Custom mask loss

Ground truth masks can be noisy so loss funcions which are more robust to noise were tested.

Soft Dice Loss

$L_{dice}(\bf{y}, \bf{\hat{y}}) = 1- \frac{2|\bf{y}\cap\bf{\hat{y}}|}{|\bf{y}|+|\bf{\hat{y}}|}$

def soft_dice_loss(pred_logits, target_masks, eps=1e-6):
    """
    pred_logits: raw logits (B, H, W)
    target_masks: binary masks (B, H, W)
    """
    pred_probs = torch.sigmoid(pred_logits)
    intersection = (pred_probs * target_masks).sum(dim=(1, 2))
    union = pred_probs.sum(dim=(1, 2)) + target_masks.sum(dim=(1, 2))
    dice_score = (2. * intersection + eps) / (union + eps)
    return 1 - dice_score.mean()

Label Smoothing BCE

def label_smoothing_bce_loss(pred_logits, target_masks, smoothing=0.05):
	"""
	Apply label smoothing to target_masks before BCE.
	"""
	target_smoothed = target_masks * (1 - smoothing) + 0.5 * smoothing
	return F.binary_cross_entropy_with_logits(pred_logits, target_smoothed)

Reduce confidence in ground truth masks.

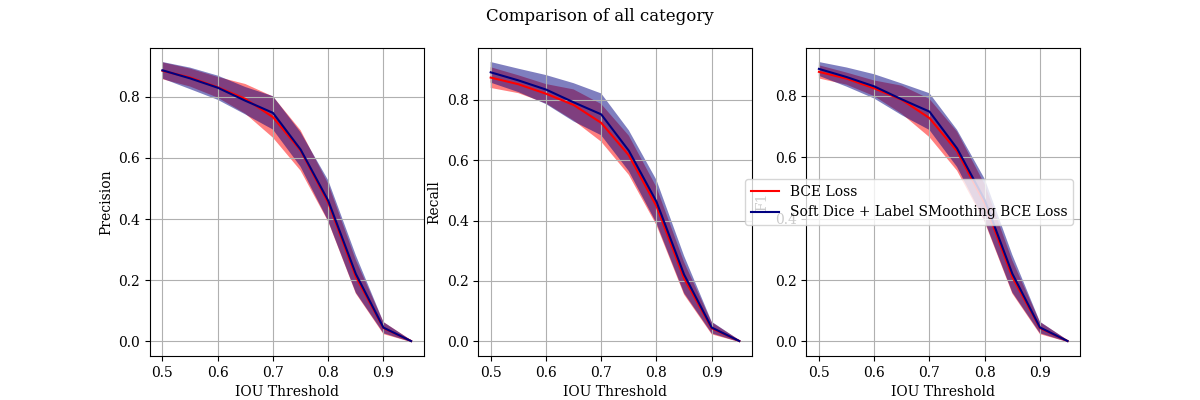
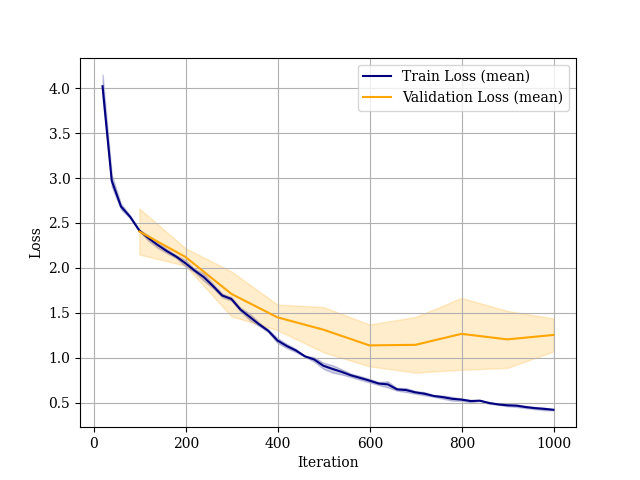
Results

No significant improvement was observed in the resulting precision recall curves.